
Index
- Introduction
- Space Segment
- Control segment
- User segment
- GPS accuracy
- How GPS works
- Errors
- Differential techniques
- Measuring Fault Motions with GPS
Introduction
A definition of GPS given by W. Wodden (1985) reads:
"The Navstar Global positioning System (GPS) is an all-weather, space-based navigation system under developement by the Department of Defense (DoD) to satisfy the requirements for the military forces to accurately determine their position, velocity and time in a common reference system, anywhere on or near the Earth on a continuous basis."
In a positioning satellite system, satellite locations and their orbits are continuously monitored from several observation centers around the world by the organization responsible for keeping the orbit of the satellite within acceptable boundaries. This organization also predicts the orbit of the satellite for the next 24 hours based on the actual orbit information received by the observation posts for the previous 24 hours (similar to weather predictions). The predicted orbit information for the next 24 hours is relayed to each satellite by the control organization, so that it can be sent to receivers. Satellites broadcast their orbit information as part of their radio signal structure.
GPS is a utility awaiting applications. It can provide positioning accuracies ranging from 100 metres (95% of the time), to 5 to 10 metres, to relative accuracies at the sub-meter, and sub-centimeter level. Present usage of GPS for positioning includes personal navigation (hiking, boating, hunting, driving directions etc), aircraft navigation, offshore survey and vessel navigation, fleet tracking, dredging, machine control, civil engineering, land surveying, GIS and Mapping and deformation analysis.
GPS consists of three segments:
- the space segment consisting of satellites wich broadcast the signal;
- the control segment steering the whole system;
- the user segment including many typer of receiver
GPS is managed by the JPO (Joint Program Office)
Space Segment

The space segment comprises a network of 24 satellites in near circular orbits placed at a 'nominal' altitude of 20,200 Km into six different orbital planes with a 55° inclination, (four satellites in each plane). The period is approximately 12 sidereal hours. This system provides global coverage with four to eight simultaneously observable satellites above 15° elevation at any time of the day.
Control segment

The Operational Control System (OCS) consists of a system of tracking stations located around the world. It's composed by a master control station, monitor stations and ground control stations.

The main operational tasks of the OCS are: tracking of the satellites for the orbit and clock determination and prediction, time syncronization of the satellites and upload of the data message to the satellites.
- Master Control Station (MCS): The location of the Master Control Station is at the Consolidated Space Operations Center (CSOC) at Shriver AFB, Colorado Springs, Colorado. CSOC collects the tracking data from the monitor stations and calculates the satellite orbit and clock parameters. The satellite control and system operation is also responsibility of the master control station.
- Monitor Stations: Five monitor stations are located at Falcon Air Force Base in Colorado, Hawaii, Ascension Island in the Atlantic Ocean, Diego Garcia Atoll in the Indian Ocean, and Kwajalein Island in the South Pacific Ocean. Each of the monitor stations checks the exact altitude, position, speed, and overall health of the orbiting satellites. The control segment uses measurements collected by the monitor stations to predict the behavior of each satellite's orbit and clock. The prediction data is up-linked, or transmitted, to the satellites for transmission back to the users. The control segment also ensures that the GPS satellite orbits and clocks remain within acceptable limits. A station can track up to 11 satellites at a time. This "check-up" is performed twice a day, by each station, as the satellites complete their journeys around the earth. Noted variations, such as those caused by the gravity of the moon, sun and the pressure of solar radiation, are passed along to the master control station.
- Ground Control Stations (GCS): Ground Control Stations, located in Ascension, Diego Garcia and Kwajalein, provide the means of commanding and controlling yhe satellites and uploading the navigation messages and other data. Ephemeris and clock data are calculated in the MCS and then uploaded to every GPS satellite via S-band radio links. Uploading is performed once or twice per day, if a ground station becomes disabled, prestored navigation messages are available in each satellite to support a prediction span so that the positioning accuracy degrades quite gradually.
User segment
The user segment includes the equipment of the military personnel and civilians who receive GPS signals. Military GPS user equipment has been integrated into fighters, bombers, tankers, helicopters, ships, submarines, tanks, jeeps, and soldiers' equipment. In addition to basic navigation activities, military applications of GPS include target designation, close air support, "smart" weapons, and rendezvous. With more than 500,000 GPS receivers, the civilian community has its own large and diverse user segment. Surveyors use GPS to save time over standard survey methods. GPS is used by aircraft and ships for enroute navigation and for airport or harbor approaches. GPS tracking systems are used to route and monitor delivery vans and emergency vehicles. In a method called precision farming, GPS is used to monitor and control the application of agricultural fertilizer and pesticides. GPS is available as an in-car navigation aid and is used by hikers and hunters. GPS is also used on Space Shuttles. Because the GPS user does not need to communicate with the satellite, GPS can serve an unlimited number of users.
GPS accuracy
There are several different levels of accuracy that can be achieved. The difference is equipment and techniques. In the commercial world, there have been roughly 4 generations of equipment, with some from the last three still in service. There are also different techniques, many made possible by LSI Chips and faster/cheaper microcomputers. The major difference in the accuracy level achieved today in a receiver is the processing techniques. This is driven by the error level on the range measurements.
For standalone users, the extent use of phase is a major factor. The noise on the phase is typically 1 mm, that on the range 10 cm to 1 m. Therefore the use of phase data in any one of several ways can improve the solution. The multipath is also drastically reduced for the phase measurement.
The second technique to remove errors is differential GPS. Here errors in the signal outside the antenna are observed at a reference station. Those errors are sent to the user by one of several methods. For realtime users this can be the US Coast Guards "beacon" transmitters, or a commercial system using satellite communication links or FM subcarriers etc. These are usually L1 only systems. The post processed differential user typically uses L1 and L2 data from high end receivers. Special techniques (called Kinematics) make use of the phase to achieve very high accuracies . However they normally can only be used out to ranges of 25 to 50 km. Many manufacturers of high end receivers have vendor specific real time version of this. You almost always have to have the same type of receiver at each end and a dedicated communication link.
GPS provides two basic levels of service, the Standard Positioning Service (SPS), designed for general public use and available worldwide without charge or restrictions and the Precise Positioning Service (PPS), a highly accurate military positioning, velocity and timing service which is available on a continuous, worldwide basis to users authorized by the United States. The PPS accuracy level is specified to be 16 m, spherical error probable (SEP). GPS position errors are always about twice as bad in height as along either horizontal axis. This means a horizontal error of about 10 m. The graph below lists the official current level. The actual level is much less. Horizontal errors for PPS (and SPS) in the 3-5 m range are common.Since Selective Availability was turned off, the main operational difference between the civilian and military systems (SPS vs PPS) is the availability of a L2 for real time removal of the ionosphere. Inexpensive receivers with only L1 still have to deal with the ionosphere that mainly affects the height. Even this difference is removed for the more expensive receivers that use complex techniques to track L2. The civilian (SPS) level is set by DoD policy. When the intentional degradation of accuracy was in place (called Selective Availability or SA) SPS accuracy was 100 m horizontal 5 % of the time (2 standard deviations). On May 1 2000, SA was set to a level of 0, effectively being turned off.

The graph shows the accuracy levels of all currently available systems. The vertical axis is the expected accuracy or error level, shown both in centimeters and meters. The horizontal axis is the distance along the earth's surface between the reference station and the remote user. If there is no reference station, the line is drawn all the way to 10,000 km, all over the earth.
How GPS works
The principle on which GPS is based is very simple: GPS determines distance between a GPS satellite and a GPS receiver by measuring the amount of time it takes a radio signal (the GPS signal) to travel from the satellite to the receiver.
Radio waves travel at the speed of light, so, if the amount of time it takes for the signal to travel from the satellite to the receiver is known, the distance from the satellite to the receiver (distance = speed x time) can be determined. If the exact time when the signal was transmitted and the exact time when it was received are known, the signal's travel time can be determined.
In order to do this, the satellites and the receivers use very accurate clocks which are synchronized so that they generate the same code at exactly the same time. The code received from the satellite can be compared with the code generated by the receiver. By comparing the codes, the time difference between when the satellite generated the code and when the receiver generated the code can be determined. This interval is the travel time of the code. Multiplying this travel time, in seconds, by the speed of light gives the distance from the receiver position to the satellite.
Point positioning
The geometrical principles of positioning can be demonstrated in terms of the intersection of "lines-of-position" (LOP) when considered in two-dimensions, and "surfaces-of-position" (SOP) in the case of three-dimensional positioning. There are essentially two broad categories of GPS positioning which can be described as real-time navigation and high precision carrier phase positioning. Navigation uses a minimum of four pseudorange measurements to four satellites which are used to solve for the three-dimensional coordinates of the receiver and the clock offset between the receiver oscillator and GPS system time. An extension to this mode is differential GPS (DGPS) which again uses the pseudorange observable for positioning, but also incorporates real-time corrections for the errors inherent in the measurements. The second category uses the much more precise carrier phase observations to compute baselines between two locations. Since the two carriers have short wavelengths (19 and 24 cm for L1 and L2 respectively), they cannot be used in the same manner as the pseudorange. The whole number of complete wavelengths (integer ambiguities) between the satellite and receiver must first be determined and this is carried out by post processing (static) or in Real-Time (RTK) using linear combinations of the two frequencies and differencing techniques. Differences between these two modes are becoming less distinguishable. Combining the pseudorange with the phase data reduces the noise error within the pseudorange measurement resulting in a much higher positioning accuracy. New techniques are also being developed to solve for the integer ambiguities in a single epoch leading to very high baseline positioning in real-time. These are known as on-the-fly or fast ambiguity resolution techniques have already proved to provide accuracies of less than 1 cm on moving platforms over short baselines.
There are two different ways to determine the distance between the satellite and the receiver, one utilises the C/A and/or P codes modulated onto the carrier signals, while the other is a carrier phase measurement.
GPS observables
The word observable is generally used to indicate any measurable parameter of a system.
In the GPS system there are two main observables:
- Code pseudorange, which is the "distance" between the GPS satellite at some transmit time and the receiver at some receive time. Because the transmit time and the receive time are different, it is impossible to measure the true range between the satellite and the receiver. Pseudorange measures utilises the C/A and/or P codes modulated onto the carrier signals and stand as the GPS basic observable, the onr that can be calculated with every receiver type. The GPS receiver measures the distance (pseudorange) between the satellite and the antenna by measuring the time the signal takes to propagate from the satellite to the receiver. The pseudorange is this time offset multiplied by the speed of light, therefore its calculation requires the knowledge of the exact instant of the signal sending and receiving. However, there are some problems with this: The receiver and satellite clocks are not perfectly synchronised - unless a very expensive clock is used within the receiver. This introduces a clock, or timing, offset which acts as an error on the distance to the satellite - hence the term pseudorange. This error must be computed and this is easily done since all pseudoranges to different satellites have the same clock offset during one measurement epoch. This is why 4 satellites are required for a position fix - to determine 3 coordinates (eg latitude, longitude and height, or X, Y and Z, or Easting, Northing and Height) + 1 for the clock offset. The C/A code is approximately 300 km long, and therefore raw observation can only range between 0 - 300 km. But the distance to the satellite is around 20,000 km. The observation must therefore be corrected and the actual pseudorange is some multiple of 300 km plus the raw observation.
- Carrier phase: Carrier Phase receivers measure the distance from the receiver to the satellites by counting the number of waves that carry the C/A Code signal. This method of determining position is much more accurate; however, it does require a substatially higher occupation time to attain 10-30 cm accuracy. Initializing a Carrier Phase GPS job on a known point requires an occupation time of about 5 minutes. Initializing a Carrier Phase GPS job on an unknown point requires an occupation time of about 30-40 minutes. This process is based on the comparison between:
1. the received carrier (broadcast bythe satellite, it has variabile frequency becaude of the Doppler shift introduced by the relative motion of the satellite and the receiver);
2. the phase of a carrier generated by an oscillator in the GPS receiver (nominally constant frequency).
What is measured is the difference between the two carriers, this allows us to achieve higher accuracies in the distance measurements than those obtained with the code pseudorange techniques. On the other hand this process introduces a new unknown quantity to evaluate. The difference between the received carrier and the receiver generated one is called the carrier beat phase, the problem is that the GPS receiver cannot distinguish one cycle of a carrier from another. The receiver measures the fractional phase, and keeps track of changes to the phase. The initial phase is undetermined, or ambiguous, by an integer number of cycles N. When the receiver locks on to a satellite signal it assigns some arbitrary value to the ambiguity. From then on, the receiver counts how many complete cycles have occurred since lock on. In other words, the integer ambiguity needs to be computed only when each satellite is locked on by the receiver. Subsequent measurements are correct relative to the initial one. Terms often associated with the carrier phase measurement are loss of lock and cycle slip. Loss of lock is as it sounds and the receiver must lock on to the satellite again and assign a new arbitrary value to the integer ambiguity. A cycle slip is when the receiver loses count of the complete number of wavelengths and therefore measurements are no longer correct relative to the initial one.
Errors
When surveying with one must consider the existence of a large set of error sources. Either the time and the phase measurements are affected by systematic errors and non random biases. Generally error sources can be divided into three groups:
- satellite related errors (clock error and orbit determination errors);
- atmosphere related errors (ionospheric and tropospheric delay);
- receiver related errors (antenna phase center variations, clock error, multipath).

Clock error
The satellites and receivers both need very good clocks to do their job. The smallest error can throw off the "range measurement" from the receiver to the satellite by many 10's, 100's or even 1000's of metres. For example a 10 nanosecond (0.00000001 sec) error would cause a 3-meter error in the range.
Satellite clock
GPS satellites use atomic clocks (cesium and rubidium oscillators) which have stabilities of about I part in 10E13 over a day. Every GPS satellite has at least three atomic clocks on-board, one that is currently active and two to three others that provide redundancy. Each atomic clock costs about $50,000 and weights more than 20kg, making not putting them in civilian receivers a good idea. The typical timing errors on GPS satellites are on the order of 1 nanoseconds every three hours, to eliminate it clocks are continuously monitored by earth stations. Clock offsets are compared using some control systems (master control clock systems) that are generated by combining more than 10 very accurate atomic clocks. Errors are then computed and included in the navigation messages. Even after treatment, some imprecision remains in the determination of satellite clock errors: tipically this translates to an effective pseudorange error of about 1m.
Receiver clock
On receivers, which need to be inexpensive, one cannot have an Atomic Clock and simple quartz clocks are supplied. Therefore, because you don't have an atomic clock, receiver's clock biases are a major source of error. This is because your receiver says it receives a signal at a specific time, but that time is in error by your receivers clock bias. This translates directly into a ranging error to that satellite, giving you an error in your position. It's not possible to expect the synchronization between satellite and receiver clocks to keep constant in time: there will always be an offset. Since any clock error or offset would affect all measurements, the computer looks for a single correction factor that would allow all the measurements to intersect at one point. To solve this problem a fourth satellite must be tracked. Assuming a receiver clock error of 1 millisecond every second (which means more or less 300 000 m) and assuming that the distance measurement happens exactly at the same time for every satellite in view, we can say that the measured distances will all be affected by the same 300 000 m offset. We can therefore consider the receiver clock error as a fourth unknown to deal with. Hence to solve the system one needs to track at least four satellites or, if the position of a second station is well known, we can use just one satellite to continuosly calculate and correct the error (corrections are done every second).
Multipath

GPS signals are sometimes reflected off nearby objects, particularly metallic objects, creating false or erroneous results. This phenomenon is known as multipath. Sever multipath can induce errors of many meters, while mild multipath may cause small, undetectable errors. Optimal accuracy is obtained by collecting data in an environment that is devoid of large reflective surfaces, like buildings and trees. The figure shows a situation where the signal coming from the satellite reaches the receuver through three different paths: one direct and the other two indirect. Consequently the received signals have relative phase offsets and the phase differences are proportional to the differences of the path lenghts. There is no general model of the multipath because of the arbitrarily different geometric situations. The influence of multipath, however, can be estimated by using a combination of L1 and L2 code and carrier phase measurements. The principle is based on the fact that the troposphere, clock errors and relativistic effects influence code and carrier phases by the same amount. This is not true for ionospheric refraction and multipath which are frequency dependent. Taking ionosphere-free code ranges and carrier phases and forming corresponding differences, all mentioned effects except for multipath are canceled. The residuals, apart from the noise level, reflect the multipath error. Purely from geometry it is clear that signals received from low satellite elevations are more susceptible to multipath than signals from high elevations. Note also that code ranges are more highly affected by multipath than carrier phases. Under certain circumstances the error resulting from multipath may grow to about 100 m in the vicinity of buildings. In severe cases of multipath loss of lock may occur. On the other hand, the multipath effects on carrier phases for relative positioning with short baselines should, generally, not be greater than 1 cm (good satellite geometry and a reasonably long observation interval). But even in those cases, a simple change in the height of the receiver may increase the multipath and, thus, deteriorate the results. When performing static surveys where the observation times tend to be relatively long , intermittent periods of multipath contamination are not a problem.
Configuration of satellites constellation

GPS determines positions through "trilateration" techniques, which are similar to the more commonly understood triangulation techniques. Distances are determined between a GPS receiver antenna and the orbiting satellites. The distance between each satellite and the receiver can be thought of as the radius of a large circle. The intersection of several circles helps determine the location of a point in space.
The configuration or geometric shape formed by the satellites affects how well positions can be determined. If satellites are well spread they form a good intersection. The area where the position is most likely to be forms a regular and consistent shape. If the satellites have a poor geometry, the bigger area of uncertainty makes position derivation significantly worse. The satellite configuration is quantified by the Geometric Dilution of Precision (GDOP). Many GPS receivers will display GDOP values. Lower GDOP values indicate better satellite configurations. In general, GDOPs less than 4 will give good position determinations.
An elevation mask also is important when applying differential corrections to improve position accuracy. When differentially correcting positions, common satellites must be used from the base station as well as the roving GPS field receivers. An elevation mask helps ensure that the roving unit doesn't record satellite measurements that the base unit can't see. Base stations commonly set elevation masks to 15°.
Anti Spoofing
Anti Spoofing further alters the GPS signal by changing the characteristics of the P code by mixing it with a so-called W code resulting in the Y code. It is the latter that is modulated onto the carriers and is thus designed to prevent the ability of the receiver to make P code measurements. Many receiver manufacturers have already developed techniques to still make P code measurements with only a small addition in added noise (cross correlation techniques), see for instance Talbot (1992) or Ashjaee and Lorenz (1992).
Atmospheric delay
Satellite broadcast signals travel through atmosphere for about 20 000 km before reaching the receiver. In its journey to the receiver the signal can be affected by the different electronic and density conditions it gets through. Generally two atmospheric layers are considered, they are called: ionosphere and troposfera.
Ionosphere
The ionosphere is that band of atmosphere extending from about 50 to 1000 kilometres above the earth's surface. In this layer the sun's ultraviolet radiation ionises gas molecules which then lose an electron. These free electrons in the ionosphere influence the propagation of microwave signals (speed, direction and polarisation) as they pass through the layer. The largest effect is on the speed of the signal, and hence the ionosphere primarily affects the measured range. The speed of the ranging codes is decreased (the so-called "group velocity") and therefore the pseudo-range is considered "delayed", and hence the range (or group) refractive index is greater than unity. (The ranging codes modulated on the carrier waves are considered a "group" of waves because they have different frequencies). The implication is therefore that the distance as implied by the integrated carrier phase is too short, but the pseudo-range is too long. The correction terms are, of course, quantities with a reversed sign, that is, the carrier phase correction is positive, while the pseudorange correction is negative. The size of the phase advance or group delay is also a function of the carrier frequency: the highest is the frequency, the smaller the effect. This behaviour of the ionosphere is called dispersion and can be put to good advantage. By making measurements on two widely spaced frequencies we can actually remove almost all of the ionospheric effect. It is for this reason that GPS satellites transmit signals on two carrier frequencies L1 at 1575,42 MHz and L2 at 1227,60 MHz.
Troposphere
On its way to the receiver, the signal must travel through the tropospheric layers of atmosphere. Troposphere is a nondispersive medium extending from the earth surface to a height of about 50 km. The troposphere's nondispersive nature delays the arrival of the carrier phase and the carrier modulation of both the L1 and L2 signals by the same amount. This depends on tropospheric refraction index, which is dependent on temperature, humidity and pressure. On the shortest path through the troposphere (the one in the Zenith direction) the time delay results in an increase in measured apparent range of about 2.4 meters. The delay grows with increasing zenith anglr and reaches 25 m for elevations of about 5°. As we said tropospheric delay cannot directly be measured using the GPS signal themselves, therefore we must resort to modeling. Troposphere is divided into to parts: a dry component, which causes about the 90% of the total rifraction and a wet component, responsible for the remaining 10%. For modeling we need measures of temperature, humidity and pressure, together with the elevation angle of the satellites. Models propsed by Hopfield, Black and Saastamoninen calculate the delay due to the dry component with an approximation of about 1 cm and tho one due to the wet part with an approximation of about 5 cm.
Differential techniques
When using phase measurements to determine a relative positioning it is always suitable, during the data adjustment stage, to use some observation combinations to reduce the number of unknowns to calculate and to reduce errors. Usually three differential techniques are adopted, they are called: single, double and triple differences.
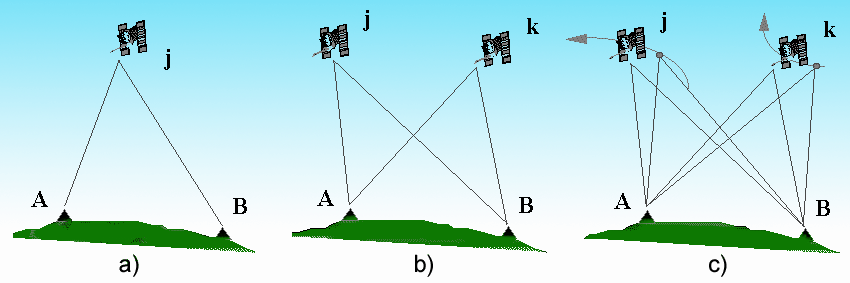
Single differences
Given two receivers called A and B tracking the same satellite j (fig. a), one can eliminate the disturb terms in the observation equations (biases or clock instabilities) by applying the single differences method. If the stations are close enough (so close that the signal passes through the same atmospheric layers to reach both A and B) one can also reduce, using this technique, the tropospheric and ionospheric refraction effects on radio signal propagation. In the same way it's possible to remove the receiver clock error by applying the single differences method to the contemporaneous observation of two satellites from one receiver.
Double differences
Double differences are obtained by simultaneously differencing between two receivers A and B and two satellites j and k (fig. b). Combining these two single differences you can cancel completely the effects of variations in the station clocks.In this case the observations are just as accurate with low-cost crystal oscillators as with an atomic frequency standard (though the use of the latter may make editing a bit easier). If the number of receivers and satellites in view and the number of observations is increased, a redundant system is generated with more observations than unknowns: this can be solved with statistic algorithms that can minimize the observation errors effect on the final values of the baselines.
Triple differences
In order to provide the maximum sensitivity to geometric parameters, the carrier phase must be tracked continuously throughout an observing session. If there is an interruption of the signal, causing a loss of lock in the receiver, the phase will exhibit a discontinuity of an integer number of cycles. This discontinuity may be only a few cycles ("cycle-slips") due to a low signal-to-noise ratio, or it may be thousands of cycles, as can occur when the satellite is obstructed at the receiver site. Initial processing of phase data is often performed using time differences of doubly differenced phase ("triple differences", or "Doppler" observations) in order to obtain a preliminary estimate of station or orbital parameters in the presence of cycle slips. Triple differences are obtained by differencing in time two double differences relative to the same couple of receivers A and B and satellites j and k (fig. c). This observable is somehow affected by more noise than the double differences observable, therefore generally the site coordinates obtained with the triple differences method are less precise than those computed with the double differences.
Measuring Fault Motions with GPS
To monitor fault motions we measure how stations near active faults move relative to each other.
When we occupy several stations at the same time, and all stations observe the same satellites, the relative positions of all the stations can be determined very precisely. Often we are able to determine the distances between stations, even over distances up to several 100 miles, to better than 5 millimeters.
Months or years later we occupy the same stations again. By determining how the stations have moved we calculate how much strain is accumulating and which faults are slipping.



